안녕하세요 코북입니다. 선형 회귀 기초입니다.
▶ Linear Model (Regression)
회귀 : 돌아서 자기 자리로 오려고 하는 것
지도 학습 -> 분류 -> KNN / Tree모델
-> 회귀 -> 선형 회귀

▶ 회귀 (Regression)
- 분류보다 회귀를 많이 사용
- 오랜 기간동안 현대 통계학에서 발생되어 다양하게 이용되는 학문분야
ex) 주식, 집값, 출산율

▶ 선형 모델 (Linear Model)
- 입력 특성에 대한 선형 함수를 만들어 예측을 수행
- 다양한 선형 모델이 존재한다
- 분류와 회귀에 모두 사용 가능 -> 선이라는 도구는 어디서든 이용 가능하다
▶ 용어 정리
y = ax + b
a : 기울기(y증가량/x증가량) -> 가중치 in ML
b : 편향(=위치) -> 절편 in ML
▷ 선형 회귀 함수
y= w1x1 + w2x2 + w3x3 + ... + wpxp + b
- x : 입력 데이터
- w : 가중치(weight) 예측값에 얼마나 영향을 미칠 건지, 계수(coefficient)
가중치가 0에 가까울수록 특성의 영향이 적다
- b : 편향 (bias), 절편 (intercept)
- 모델 w파라미터 : model.coef_
- 모델 b파라미터 : model.intercept_
▷ 머신러닝 기법에서의 선형 회귀
--> 주어진 특성(x)과 결정 값 데이터(y)에 기반하여,
학습을 통해 최적의 회귀 계수(W,b)를 찾아내는 것

▷ Cost function (비용함수 : 수식을 검증)
- 원데이터 = y
- 예측값 = H(x) = w*x+b
- 오차 = H(x) - y (예측값 - 원래 값)
-> +, - 값이 섞여있기 때문에 오차를 모두 더할 때는 제곱 값 사용!
▷ Why 절대값은 왜 안 써?
1. 제곱을 통해 커진 값들이 오차를 발견하기에 더 적절하다 (시각화에 유리)
2. 코딩적으로 봤을 때, 절대값을 구하려면 '+'인지 '-'인지 알기 위한 처리를 한 번 더 해줘야 한다
▷ 평균제곱오차 (MSE : Mean Squared Error)
- 오차를 제곱해서 평균을 낸다
- 일반적으로 선형 회귀에서 사용하는 평가지표
--> 평균제곱오차(MSE)가 가장 적은 직선을 찾는다
▷ 평균제곱근오차 (RMSE : Root Mean Squared Error)
- 평균제곱오차에 루트를 씌워 값을 다시 낮춰준다 -> 원래 단위로 맞춰줌
RMSE/MSE의 단점
- 예측 대상의 크기에 영향을 받음
ex) 삼성전자 주가 2,389,000 / 네이버 주가 778,000
삼성전자와 Naver의 주가 예측 RMSE가 500,000이 나왔다면 두 모델의 성능이 동일할까요?
No -> 삼성전자에서 더 정확함. 값 자체의 비율을 비교했을 때,
네이버에서 778,000 중 500,000이기 때문에 삼성보다 훨씬 큰 오차라고 볼 수 있다

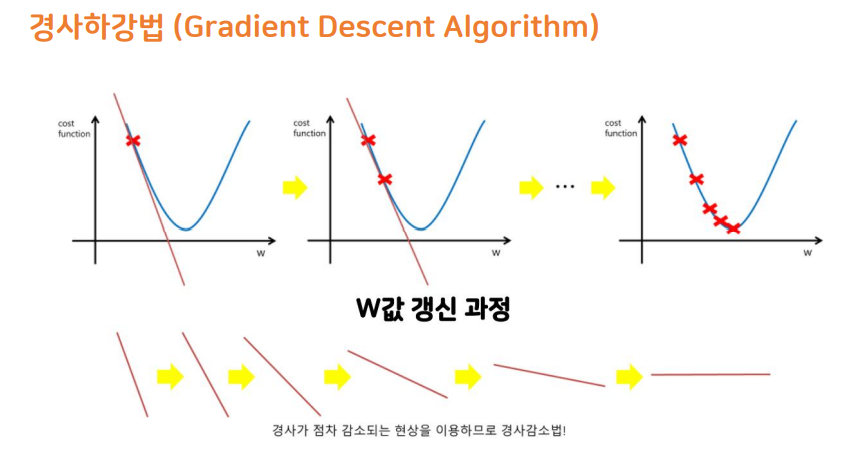
▶ 경사하강법 (Gradient Descent Algorithm)
비용 함수의 기울기(경사)를 구하여
기울기가 낮은 쪽(MSE가 가장 적은 w값)으로 계속 이동하여 값을 최적화시키는 방법
오차가 낮은 부분을 찾아야하는데 어떻게 찾아가는가?
-> 오차가 0인 부분의 특징 : 기울기 = 0
-> 경사하강법 사용 : 경사(기울기)가 점차 감소되는 현상을 이용하므로 경사 감소법

▷ Learning rate (학습률)-> 학습량을 조절하는 파라미터
한 번에 얼마나 학습량을 수정할 지 정하는 파라미터
- Learning rate가 큰 경우
1. 놓치는 지점이 발생할 가능성이 커짐, 최적점을 놓칠 확률이 높음
2. 발산할 수 있음
- Learning rate가 작은 경우
1. 시간이 너무 오래걸린다
2. 그래프 중간에 위치한 Local minimum을 최저값이라고 판단하여 학습이 멈출 수 있다
▶ Linear Model 장점
- 결과예측(추론) 속도가 빠르다 -> 수식이 만들어져 있다면 대입해서 계산만 하면 되기 때문에
- 대용량 데이터에도 충분히 활용 가능하다
- 특성이 많은 데이터 세트라면 훌륭한 성능을 낼 수 있다
▷ 비교
KNN -> 흩어져 있는 데이터를 분석하는 것이기 때문에 예측 속도가 오래 걸림
▶ Linear Model 단점
- 특성이 적은 저차원 데이터에서는 다른 모델의 일반화 성능이 더 좋을 수 있다
-> 특성확장을 하기도 한다
- LinearRegression Model은 복잡도를 제어할 방법이 없어 과대 적합되기 쉽다
-> 오차를 줄이기 위한 처리들이 과대적합을 유발할 수 있다
-> 모델 정규화(Regularization)을 통해 과대 적합을 제어한다

▶ 선형 모델 정규화 방법
비용함수 + 정규화 항
정규화란 가중치가 가질 수 있는 값에 정규화 항을 이용해 제약조건을 부여하는 방법
제약조건은 일반적으로 가중치의 크기를 제한하는 방법
▷ 모델 정규화
가중치(w) 값을 조정하여 제약을 주는 것
규제 : 모든 특성이 출력에 주는 영향을 최소한으로 만듦
- L1규제 : Lasso
가중치의 절대값을 이용
w의 모든 원소에 똑같은 힘으로 규제를 적용하는 방법.
특정 계수들은 '0' 이 됨. 0이 될 수 있다는 점이 Ridge와 다르다
특성 선택(Feature Selection)이 자동으로 이루어진다.
- L2규제 : Ridge
가중치의 제곱값을 이용
w의 모든 원소에 골고루 규제를 적용하여 '0'에 가깝게 만든다
0이 되지 않는다는 것이 포인트
--> MSE(평균제곱오차)를 구하기 위한 기준(람다=규제의 강도)이 하나 더 생겼다고 보면 된다

▷ 하이퍼파라미터(alpha) 탐색
- 값이 조금 변해도 모형 동작이 크게 변하지 않음
- 값을 크게 바꿔가며 탐색
ex) 10배씩 늘려가며 시도 e.g) 0.01, 0.1, 1, 10, 100,...
'Machine Learning' 카테고리의 다른 글
| [LinearRegression] 서울시 구별 CCTV현황 분석과 특성공학 (0) | 2021.09.14 |
|---|---|
| [Kaggle] 전자 상거래 물품 배송 예측(분류) (0) | 2021.09.10 |
| [MachineLearning] 머신러닝 개요 (0) | 2021.09.01 |
| [MachineLearning] 머신러닝과 기초통계학 (0) | 2021.08.31 |
![[LinearRegression] 선형 회귀 기초](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbbWLvo%2Fbtre099luIR%2FAAAAAAAAAAAAAAAAAAAAAHiPfyud1YjTmTRVA5T2tiLFk4O5VRQZQKcVvvtNGoTV%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DK2f8hXfFbRoLtCC%252BeIrdJqs6oN0%253D)